A análise de um mecanismo de forma geral pode se tornar bastante complexa no que diz respeito ao equacionamento de seus deslocamentos, velocidades e acelerações, à medida em que aumentamos o número de barras na sua constituição, principalmente se utilizarmos os métodos de posicionamento – coordenadas cartesianas – comuns na mecânica clássica. A esse respeito vamos introduzir o conceito de coordenadas generalizadas no posicionamento das diversas barras de um mecanismo, simplificando e permitindo uma análise cinemática bastante concisa de forma geral.
1. Coordenadas Generalizadas
A configuração de um sistema mecânico em que todos os corpos envolvidos tenham movimento plano ou espacial, com um número finito de corpos rígidos, pode ser expressa por um número finito de variáveis reais chamadas coordenadas generalizadas. Cada corpo rígido, no plano, poderá ser denotado por três coordenadas generalizadas ou por seis coordenadas no espaço, percebendo-se que no plano este tem três graus de liberdade, sendo possíveis dois deslocamentos e uma rotação. No espaço seriam seis, constituídos por três deslocamentos e três rotações. Assim, é fácil a obtenção das variáveis do sistema quando todos os corpos estiverem livres. Para as situações em que isto não ocorre, o sistema pode ser simplificado (reduzido) após a determinação das equações de restrição como visto à frente. Este sistema geral de coordenadas generalizadas será indicado por:
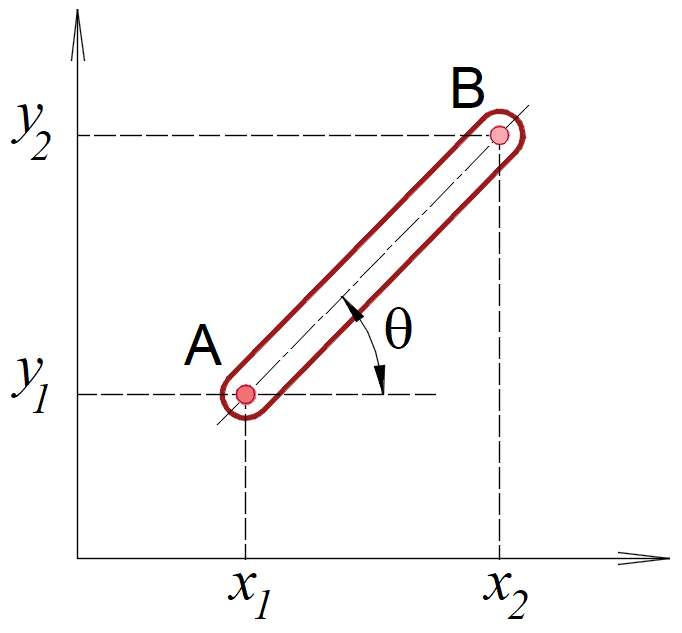
(x_1, x_2, x_3,\cdots,x_n) \tag{1}Como exemplo, o sistema mostrado na figura 1 pode ser descrito com a utilização do ângulo θ que a barra AB forma com a horizontal e das coordenadas x e y de um ponto qualquer na barra.
Nesta situação, as coordenadas generalizadas seriam ($x, y, \theta$). Também poderíamos descrevê-lo utilizando as coordenadas cartesianas de dois pontos distintos da barra e o sistema de coordenadas generalizadas seria então dado por ($x_1, y_1, x_2, y_2$).
Observe:
Deve ser evitado, no sistema de coordenadas generalizadas inicial, variáveis que sejam constantes. Isto só deve acontecer como consequência de restrições futuras.
1.1. Restrições
Pontos materiais de um sistema mecânico ou de partículas podem estabelecer vínculos entre si, através de fixações ou ligações móveis entre dois ou mais corpos, que impõem limitações aos seus deslocamentos. Estes vínculos também são chamados restrições. Observe porém que se houver uma ligação entre dois corpos pertencentes ao sistema, do tipo soldagem, ou seja, sem que haja a partir dai possibilidade de movimento relativo entre eles, isto não será uma restrição e sim uma transformação de dois corpos em um único no referido sistema que passa a ter um corpo a menos. Neste caso serão geradas equações de restrição, subentendemos que ai houve uma “restrição virtual”.
Se a restrição puder ser equacionada com a utilização de coordenadas generalizadas, e eventualmente também do tempo quando uma ou mais variáveis que compõe o sistema for temporal, de tal forma que se possa ter como verdadeira a equação 2 a seguir:
f(x_1,x_2,x_3,\cdots,x_n)=0 \tag{2}ela será dita holonômica, caso contrário será chamada não-holonômica, como é o caso dos mecanismos com base em órgãos de tração ou compressão como especificado na classificação de Releaux.
Saiba mais:
Sistemas com órgãos não rígidos onde não se pode prever expansões ou contrações devidas à dilatação térmica no tempo são sempre não-holonômicos.
1.2. Graus de Liberdade de um Sistema Mecânico
Determinado convenientemente, um sistema de coordenadas generalizadas para um sistema mecânico de corpos rígidos em que as restrições, se houver, sejam todas do tipo holonômicas, define-se o número de graus de liberdade do sistema através da seguinte relação:
f=n-r \tag{3}Onde:
f – número de graus de liberdade do sistema;
n – número de coordenadas generalizadas usadas para descrever o sistema;
r – número de equações de restrição existentes no sistema de coordenadas generalizadas adotado.
Desta forma, o número de graus de liberdade é uma característica intrínseca do sistema e independe do sistema particular de coordenadas utilizado para sua descrição. Apenas ressalte-se que o número de equações de restrição será diferente de um sistema para o outro, desde que os mesmos tenham número de coordenadas diferentes. Em particular, é possível se achar um conjunto de coordenadas independentes tal que o número de equações de restrição, neste sistema, seja nulo.
Neste ponto se faz interessante o leitor perceber a singeleza, simplicidade e também exatidão do tratamento matemático que vai permitir a obtenção do número de graus de liberdade para qualquer tipo de sistema de corpos rígidos, a despeito da idéia intuitiva para tal fim, que se coloca nos compêndios de mecânica geral. Também, apesar de estarmos dando enfoque a sistemas de corpos rígidos no plano, é fácil perceber que tal tratamento pode ser estendido aos sistemas espaciais sem nenhuma dificuldade.
Como exemplo elucidativo, vamos considerar uma haste, figura 3, no plano bidimensional ($x, y$) com uma extremidade fixa em ($x_0, y_0$) e com capacidade de rotacionar em torno deste. Na outra extremidade desta haste coloca-se uma segunda através de um pivô rotativo que permite giro entre as duas.
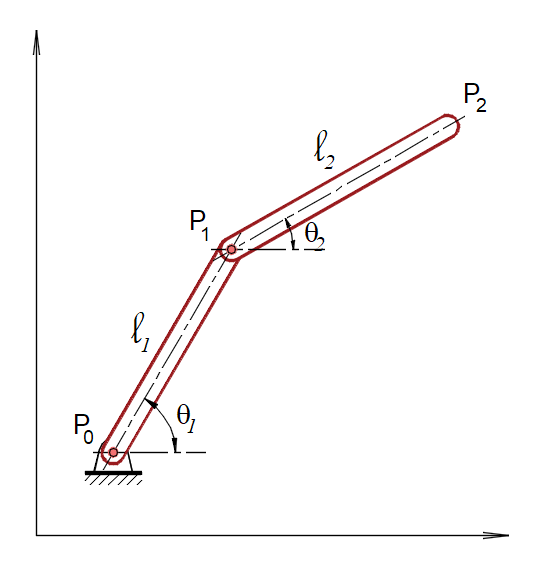
A configuração do sistema será então dada por quatro coordenadas $x_{p_1}, y _{p_1} , x _{p_2}$ e $y _{p_2}$ e, para este caso, o número de equações de restrição é dois:
\begin{aligned} (x_{p_0}-x_{p_1})^2+(y_{p_0}-y_{p_1})^2 &=\ell_1 \\ (x_{p_1}-x_{p_2})^2+(y_{p_1}-y_{p_2})^2 &=\ell_2 \end{aligned} \tag{4}Note que aqui $x_{p_0}, y_{p_0}$, são constantes que podem ser utilizadas livremente nas equações de restrição, logo o número de graus de liberdade do sistema será:
f=n-r=4-2=2 \tag{5}Poderíamos também utilizar como coordenadas generalizadas os ângulos $\theta_1$ e $\theta_2$ que as barras fazem com a horizontal e, neste caso, ficaríamos sem nenhuma equação de restrição envolvendo estas coordenadas.
Saiba mais:
Se o sistema de coordenadas generalizadas escolhido for linearmente independente, o número de equações de restrição será sempre nulo.
2. Exemplo Prático
Vejamos agora um exemplo mais clássico que irá consistir na formação do mecanismo biela-manivela que iremos estudar futuramente em detalhes. Sejam portanto três corpos rígidos, livres no plano, como mostrado na figura 4a, e descritos pelo sistema de coordenadas generalizadas da equação 6 a partir da geometria de posicionamento montada na figura 4b.
(x_1,x_2,x_3,y_1,y_2,y_3,\alpha,\varphi,\delta) \tag{6}
Vamos agora criar quatro restrições para este sistema, figura 5, consistindo de um pivotamento na coordenada ($3,5$) do plano para o ponto $P_1$, vínculo A, um pivotamento entre o corpo 1 e o corpo 2, vínculo B, um pivotamento entre o corpo 2 e o corpo 3, vínculo C, e vamos excluir o deslocamento angular e deslocamento na direção y para o corpo 3, ficando este sempre na coordenada y = 3, vínculo D.

Desta forma, o vínculo A, permitindo que o corpo 1 apenas rotacione na coordenada (3,5) cria as duas restrições da equação 7.
\begin{aligned} x_1 &= 3\\ y_1 &= 5 \end{aligned} \tag{7}O vínculo B, ligando o corpo 1 ao corpo 2 por uma rotação relativa cria as duas restrições da equação 8.
\begin{aligned} \ell_1 \cos\alpha+\ell_2\cos\varphi-x_2+x_1 &= 0\\ \ell_1 \,\text{sen}\,\alpha-\ell_2\,\text{sen}\,\varphi-y_2+y_1 &= 0 \end{aligned} \tag{8}O vínculo C, ligando o corpo 2 ao corpo 3 por uma rotação relativa cria as duas restrições da equação 9.
\begin{aligned} x_2 &= x_3\\ y_2 &= y_3 \end{aligned} \tag{9}O vínculo D, limitando o corpo 3 apenas a deslocamentos lineares a uma altura de 5 unidades do eixo horizontal (coordenada 5), cria também duas restrições mostradas na equação 10.
\begin{aligned} \delta &= 0\\ y_3 &= 5 \end{aligned} \tag{10}Somando-se as equações mostradas em (7), (8), (9) e (10) obtém-se o valor 8 e, considerando que a quantidade de coordenadas generalizadas inicialmente propostas na equação (6) foi de 9, vai-se obter para o número de graus de liberdade do novo sistema um valor unitário, como mostrado na equação 11.
f=n-r=9-8=1 \tag{11}O processo aqui utilizado para a obtenção do número de graus de liberdade se torna muito complexo, ou até inviável, para sistemas contendo muitas barras, por isto serão desenvolvidas, mais à frente, expressões que irão simplificar o processo.
