11. Trens epicicloidais
11.1 Relação para os Trens Epicicloidais
Neste tipo de trem, há um eixo, simples ou composto que gira em torno de um eixo de referência, as engrenagens neste eixo são conhecidas como planetas e sobre o eixo de referência, elas levam o nome de sol ou anel, conforme sejam externas ou internas respectivamente.

Originariamente este trem vai ter dois graus de liberdade e, consequentemente, será necessária a fixação de pelo menos uma engrenagem ou o braço para que o transformemos em um mecanismo passível de análise.
Em função da geometria, tem-se aqui os trens planetários e os trens diferenciais.
11.2 Nomenclatura
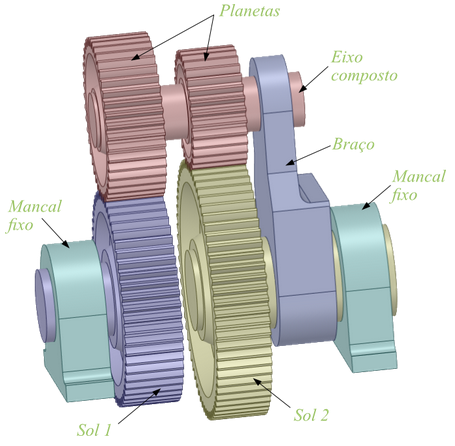
Os sois, quando se tornam engrenagens internas, passam a receber o nome de anel e o sistema passa a se chamar “Trem Planetário”
Pela figura, é perceptível que o sistema tem dois graus de liberdade e o seu funcionamento, como mecanismo, só é possível quando for fixado um dos três elementos seguintes:
- Braço
- Sol 1
- Sol 2
11.3 Relação Virtual
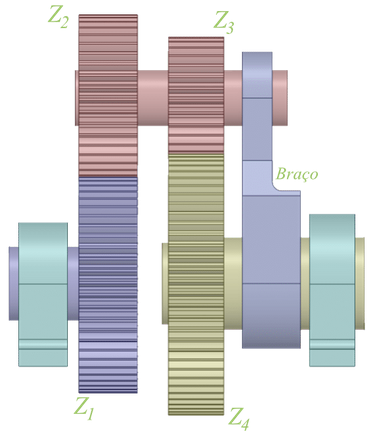
Percebam que um observador no braço veria este como fixo e, consequentemente perceberia apenas um trem composto em movimento.
Portanto, considerando velocidades relativas.
\[ \frac{ \omega_{4B} }{ \omega_{1B} }\,=\,\frac{z_1 z_3}{z_2 z_4} \]
E é possível se construir então a equação “virtual”:
\[ \frac{ \omega_B – \omega_4 }{ \omega_B – \omega_1 }\,=\,\frac{ z_1 z_3 }{ z_2 z_4 } \tag{11.1} \]
11.4 Transmissão com o braço fixo
Como já relatado, o sistema vai se comportar como em um trem composto.

\[ \varphi_{14} \,=\, \frac{z_1 z_3}{z_2 z_4} \tag{11.2} \]
11.5 Sol 1 (Engrenagem 1) Fixo
Neste caso, eliminamos a velocidade da engrenagem 1 na equação virtual e buscamos pela relação \(\varphi_{4B}\), se a entrada se fizer pelo sol 2.
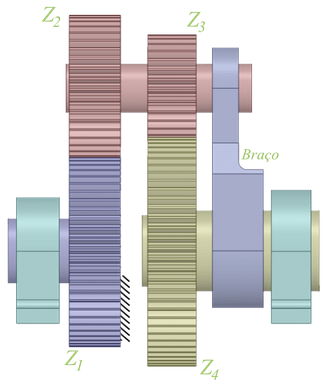
\[ \varphi_{4B} = \frac{ \omega_B }{ \omega_4 } = \frac{ z_2 z_4 }{ z_2 z_4 – z_1 z_3 } \tag{11.3} \]
Ou pela relação \(\varphi_{B4}\), se a entrada se fizer pelo braço.
\[ \varphi_{4B}=\frac{\omega_4}{\omega_B}=1-\frac{z_1 z_3}{z_2 z_4} \tag{11.4}\]
11.6 Sol 2 (Engrenagem 4) Fixo
Neste caso, eliminamos a velocidade da engrenagem 4 na equação virtual e buscamos pela relação \(\varphi_{1B}\), se a entrada se fizer pelo sol 1.

\[ \varphi_{1B} = \frac{ \omega_B }{ \omega_1 } = \frac{ z_1 z_3 }{ z_1 z_3 – z_2 z_4 } \tag{11.5} \]
Ou pela relação \(\varphi_{B1}\), se a entrada se fizer pelo braço.
\[ \varphi_{B1}=\frac{\omega_1}{\omega_B}=1-\frac{z_2 z_4}{z_1 z_3} \tag{11.6}\]
11.7 Exercícios
- No trem hepicicloidal, mostrado abaixo, as engrenagens 2 e 3 têm a mesma quantidade de dentes, a engrenagem 1 tem z-1 dentes e engrenagem 4 tem z dentes (esta montagem é possível, se os pares 1-2 e 3-4 tiverem módulos diferentes). Conhecida a velocidade angular da engrenagem 1 e, sendo a entrada pelo braço e saída pela engrenagem 4, verifique se a relação de transmissão pode ser dada pela equação:
\varphi(\omega_1,\omega_B)=\frac{1}{z}(1-\frac{\omega_1}{\omega_B})
- Para o trem de engrenagens mostrado na figura abaixo, são compostas, duas a duas, as engrenagens 2-3, 4-5, 6-7, 8-9 e 1-10. A entrada se faz pelo eixo A e a saída se dá pelo eixo B ligado ao braço. Determine a relação de transmissão, quando a engrenagem 2 for igual à engrenagem 3 em número de dentes e módulo.

