Perfil do Came

     A bem pouco tempo atrás a usinagem do perfil dos cames se dava em fresas universais de pouca precisão a despeito disto, com relação ao movimento do seguidor, o jerk se fazia notar mesmo para curvas de elevação de alto desempenho, onde os efeitos teóricos de jerk não existiam, Felizmente, hoje em dia os sistemas de fabricação baseados em centrais de usinagem de alta precisão vieram corrigir este problema, porém estes sistemas demandam expressões matemáticas mais acuradas predizendo com a máxima eficiência a geometria da peça.

     Se faz necessário entretanto, para estes sistemas, que forneçamos as equações que irão predizer o caminho das ferramentas com a máxima exatidão. O Flores [N/A], nos apresenta uma maneira de obter estas equações, porém de forma bastante complexa, Nos tópicos a seguir, proporemos um método bastante simplificado para a obtenção das equações cartesianas parametrizadas que irão possibilitar a obtenção, não só do contorno da curva primitiva no came, como também do seu perfil e caminho da ferramenta de usinagem.

2. Perfil da Curva Primitiva

     Neste ponto, devemos considerar já conhecidas as expressões que compõem a curva completa de elevação e repouso $f(\theta)$, figura 1 e também o raio $R_p$ da circunferência principal.

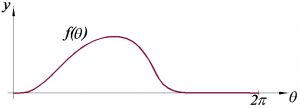
Figura 1 – Diagrama completo – Elevação-Retorno-Repouso (E-R-Rp).

     Desta forma é suficiente que passemos o diagrama da figura para coordenadas polares considerando um adendo devido ao raio da circunferência principal, obtendo as coordenadas ($\rho$, $\theta$), onde $\rho=R_p+f(\theta)$ e, pela figura 2 Vemos que as equações cartesianas paramétricas $(u,v)$ são imediatas.
$$\begin{equation} \left\{ \begin{array}{ll} u = [R_p+f(\theta)]\cos\theta \\ v = [R_p+f(\theta)]\,\text{sen}\,\theta \end{array} \right. \end{equation}$$

Figura 2 – Contorno da Curva Primitiva

     Apesar de corretas, estas equações traçam um contorno de curva primitiva ligeiramente rotacionado em relação ao eixo vertical, ou seja o eixo de simetria do came não coincide com o eixo das ordenadas, mas isto pode ser resolvido por uma simples rotação do sistema de coordenadas $uv$ de um ângulo “$\delta$” no sentido horário, veja na figura 3.

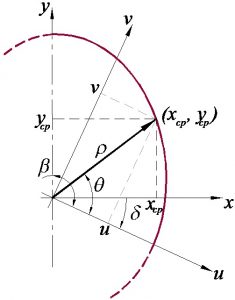
Figura 3 – Contorno da Curva Primitiva Alinhada

     Para este caso, verificando que o ângulo $\delta$ é negativo, as novas coordenadas podem ser obtidas, de acordo com a álgebra linear, por uma simples rotação do sistema:

$$\begin{equation} \left\{ \begin{array}{c} x_{cp} \\ y_{cp} \end{array} \right\} = \left[ \begin{array}{lr} \cos{(-\delta)} & -\text{sen}{(-\delta)} \\ \sin{(-\delta)} & \cos{(-\delta)} \end{array} \right] \cdot \left\{ \begin{array}{c} u \\ v \end{array} \right\} \end{equation}$$

     E, notando pela figura~ContPrimitAlinhado, que $\delta=\beta-\frac{\pi}{2}$, teremos $\cos{(-\delta)} = \cos{(\frac{\pi}{2}-\beta)} = \sin\beta$ e $\sin{(-\delta)} = \sin{(\frac{\pi}{2}-\beta)} = \cos\beta$, também substituido os valores de $u$ e $v$ obtidos acima, vem:

$$\begin{equation} \left\{ \begin{array}{c} x_{cp} \\ y_{cp} \end{array} \right\} = \left[ \begin{array}{lr} \sin\beta & -\cos\beta \\ \cos\beta & \text{sen}\,\beta \end{array} \right] \cdot \left\{ \begin{array}{c} [R_p+f(\theta)] \cos\theta \\ [R_p+f(\theta)] \text{sen}\,\theta \end{array} \right\} \end{equation}$$

     Rearrumando a equação 3, ficamos com:

$$\begin{equation} \left\{ \begin{array}{ll} x_{cp} = [R_p+f(\theta)](\text{sen}\,\beta \cos\theta-\text{sen}\,\theta \cos\beta) \\ y_{cp} = [R_p+f(\theta)](\cos\beta \cos\theta+\text{sen}\,\beta \,\text{sen}\,\theta) \end{array} \right. \end{equation}$$

     Que finalmente pode ser reescrita:

$$\begin{equation} \left\{ \begin{array}{ll} x_{cp} = [R_p+f(\theta)]\, \text{sen}(\beta-\theta) \\ y_{cp} = [R_p+f(\theta)] \cos(\beta-\theta) \end{array} \right. \label{XcpYcp_em_Teta} \end{equation}$$

     No problema anterior, também poderíamos ter obtido o contorno da curva primitiva alinhado em função de um ${\theta}’$, como na figura 4, tendo o cuidado de entender que este ${\theta}’$ não é o $\theta$ utilizado no diagrama de elevação.

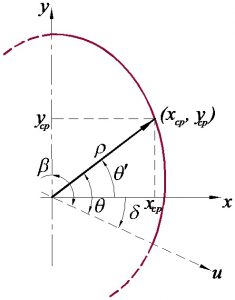
Figura 4 – Curva Primitiva Alinhada por $\theta’$

$$\begin{equation} \left\{ \begin{array}{ll} x_{cp} = [R_p+f(\theta)]\cos{\theta}’ \\ y_{cp} = [R_p+f(\theta)]\,\text{sen}\,{\theta}’ \end{array} \right. \label{XcpYcp_em_TetaLinha} \end{equation}$$

     No entanto, note que $\theta={\theta}’+\delta$ e, consequentemente ${\theta}’=\theta-\delta=\theta-(\beta-\frac{\pi}2)=\frac{\pi}2-(\beta-\theta)$ e então $\cos{\theta}’=\text{sen}(\beta-\theta)$ e $\text{sen}\,{\theta}’=\cos(\beta-\theta)$, fazendo com que a equação 6 se transforme na equação 5. Posto isto, daqui para a frente, vamos utilizar a curva já alinhada com ${\theta}’=\frac{\pi}2-(\beta-\theta)$ na obtenção dos perfis do came e curvas da ferramenta de corte.

3. Perfil do Came

     A partir de agora, conhecidas as equações paramétricas da curva primitiva, vamos desenvolver estas equações para o perfil do came propriamente dito, figura 5, notando que o contato do rolete com a superfície do came se dá segundo o ângulo de pressão $\varphi$ que, como visto no capítulo 5, no caso de cames radiais tem para valor:
$$\begin{equation} \varphi(\theta)=\text{arctg}{(\frac{f'(\theta)}{f(\theta)+R_p})} \end{equation}$$

Figura 5 – Perfil Exato do Came

     Com um pouco de álgebra, a figura 5 nos permite obter:
$$\begin{equation} \left\{ \begin{array}{c} x_c \\ y_c \end{array} \right\} = \left\{ \begin{array}{c} x_{cp} \\ y_{cp} \end{array} \right\} + \left[ \begin{array}{lr} \cos\gamma & -\text{sen}\,\gamma \\ \sin\gamma & \cos\gamma \end{array} \right] \cdot \left\{ \begin{array}{c} R_r \\ 0 \end{array} \right\} \end{equation}$$

     Agora, notando que $\gamma=\pi+{\theta}’-\varphi$ e que, como visto acima ${\theta}’=\frac{\pi}2-(\beta-\theta)$, vamos obter $\gamma=\frac{3\pi}2-(\varphi+\beta-\theta)$ e $\cos\gamma=-\text{sen}(\varphi+\beta-\theta)$ e $\sin\gamma=-\cos(\varphi+\beta-\theta)$. Com isto reformulamos a última equação para:

$$\begin{equation} \left\{ \begin{array}{c} x_c \\ y_c \end{array} \right\} = \left\{ \begin{array}{c} [R_p+f(\theta)] \,\text{sen}(\beta-\theta) \\ [R_p+f(\theta)] \cos(\beta-\theta) \end{array} \right\} + \left[ \begin{array}{lr} -\text{sen}(\varphi+\beta-\theta) & \cos(\varphi+\beta-\theta) \\ -\cos(\varphi+\beta-\theta) & -\text{sen}(\varphi+\beta-\theta) \end{array} \right] \cdot \left\{ \begin{array}{c} R_r \\ 0 \end{array} \right\} \label{XcYc_Matricial} \end{equation}$$

     Ou, finalmente:

$$\begin{equation} \left\{ \begin{array}{ll} x_c = [R_p+f(\theta)] \,\text{sen}(\beta-\theta) – R_r \,\text{sen}(\varphi+\beta-\theta) \\ y_c = [R_p+f(\theta)] \cos(\beta-\theta) – R_r \cos(\varphi+\beta-\theta) \end{array} \right. \end{equation}$$

4. Came Conjugado

     No caso de cames conjugadas [N/A], figura 6, o ângulo entre a horizontal e o eixo das abscissas, no sistema local $uv$, será $\gamma={\theta}’-\varphi$, ou seja $\gamma=\frac{\pi}2-(\varphi+\beta-\theta)$, quando então $\cos\gamma=\sin(\varphi+\beta-\theta)$ e $\text{sen}\,\gamma=\cos(\varphi+\beta-\theta)$.

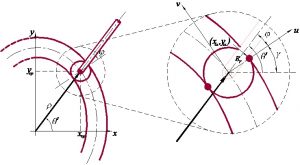
Figura 6 – Perfil do Came Conjugado

     Desta forma a matriz da transformação na equação (9) terá os dois elemento na primeira coluna positivos, fazendo com que o sinal de $R_r$ seja invertido na equação (10) e iremos obter então, para o contorno superior:
$$\begin{equation} \left\{ \begin{array}{l} x_{cs} = [R_p+f(\theta)] \,\text{sen}(\beta-\theta) + R_r \,\text{sen}(\varphi+\beta-\theta) \\ y_{cs} = [R_p+f(\theta)] \cos(\beta-\theta) + R_r \cos(\varphi+\beta-\theta) \end{array} \right. \label{Eq_ContCameSuperior} \end{equation}$$

5. Caminho da Ferramenta de Corte

     Como já foi dito anteriormente, os sistemas modernos de usinagem por CNC, requerem o caminho da ferramenta de corte ou mais precisamente as equações matemáticas que o determinam, para isto é claro precisamos saber o diâmetro da fresa e, consequentemente o seu raio $R_f$ que iremos utilizar no desenvolvimento, figura 7.

Figura 7 – Caminho da Ferramenta de Corte

     Aqui, como no caso de cames conjugadas, o ângulo entre a horizontal e o eixo das abcissas, no sistema local $uv$, será $\gamma={\theta}’-\varphi=\frac{\pi}2-(\varphi+\beta-\theta)$, e $\cos\gamma=\sin(\varphi+\beta-\theta)$ e $\text{sen}\,\gamma=\cos(\varphi+\beta-\theta)$ e a matriz coluna, contendo as variáveis locais na equação (9) será composta por $R_f-R_r$ na primeira linha e zero na segunda, ficando então:

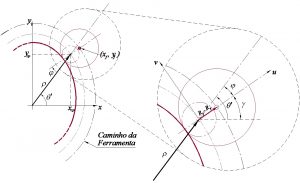
Figura 8 – Geometria para o Caminho da Ferramenta

$$\begin{equation} \left\{ \begin{array}{l} x_f = [R_p+f(\theta)] \,\text{sen}(\beta-\theta) + (R_f-R_r) \text{sen}(\varphi+\beta-\theta) \\ y_f = [R_p+f(\theta)] \cos(\beta-\theta) + (R_f-R_r) \cos(\varphi+\beta-\theta) \end{array} \right. \label{Eq_ContFerramenta} \end{equation}$$

6. Plotagem de Exemplos

     As figuras seguintes mostram a plotagem, com a utilização da equação~XcpYcp_em_Teta, da equação~Eq_ContCame, e da equação~Eq_ContFerramenta, para os perfis de came, curva primitiva e caminho da ferramenta para uma curvas clássicas e também para as duas curvas desenvolvidas neste trabalho. Os trechos de elevação e retorno simétricos com base na mesma curva de elevação, sendo para a elevação e retorno $\beta_1=\beta_2=\frac{\pi}3$ a uma altura de 20 mm para o raio da circunferência principal igual a 80 mm, raio do rolete igual a 8 mm e raio da ferramenta de corte igual a 25 mm.

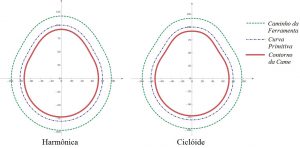
Figura 9 – Plotagem dos Perfis para as curvas Harmônica e Cicloidal

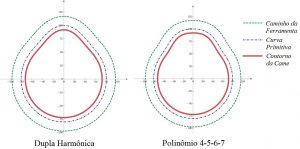
Figura 10 – Plotagem dos Perfis para as curvas Dupla Harmônica e Polinomial 4-5-6-7

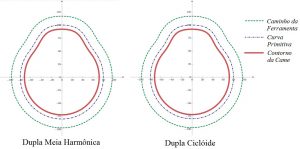
Figura 11 – Plotagem dos Perfis para as curvas Dupla Meia-Harmônica e Dupla Ciclóide

=== xxx ===