Para o desenvolvimento das curvas de elevação, em camos, vamos relembrar os conhecimentos sobre as operações que podemos fazer nas funções com a consequente mudança em seus gráficos, neste estudo, nós estamos convencionado que a função original tem azul para a cor de seu gráfico e a função obtida, pela operação indicada, tem a cor vermelha para o seu gráfico. Desta forma, vai nos interessar as seis operações seguintes:
1. Translação de função na direção horizontal (eixo x)
Figura 1 – Translação de \(a\) na direção \(x\).
A figura 1 mostra bem que a função \(g(x)\) obtida da função \(f(x)\) pela translação desta de um distância \(a\) na horizontal será:
\[g(x)=f(x-a)\]
2. Translação de função na direção vertical (eixo y)
Figura 2 – Translação de \(h\) na direção \(y\).
Na figura 2, podemos perceber que a função \(g(x)\) obtida da função \(f(x)\) pela translação desta de uma altura \(h\) na vertical será:
\[g(x)=f(x)+h\]
3. Espelhamento Horizontal (no eixo x)
Figura 3 – Espelhamento de função no eixo \(x\).
Pela figura 3, vemos que a função \(g(x)\) pode ser obtida da função \(f(x)\) pela troca do sinal na própria função \(f(x)\):
\[g(x)=-f(x)\]
4. Espelhamento Vertical (no eixo y)
Figura 4 – Espelhamento de função com relação ao eixo \(y\).
Na figura 4, é fácil ver que a função \(g(x)\) pode ser obtida da função \(f(x)\) pela troca de sinal do argumento:
\[g(x)=f(-x)\]
5. Expansão ou Contração Estritamente na Horizontal
Figura 5 – Expansão de função na direção \(x\).
A expansão ou escalonamento, figura 5, na direção x, função \(g(x)\), pode ser obtida da função \(f(x)\) pela multiplicação do argumento por um fator \(k=\frac{a}{b}\):
\[g(x)=f(\frac{a}{b}x)\]
6. Expansão ou Contração Estritamente na Vertical
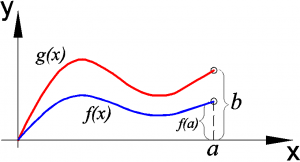Figura 6 – Expansão de função na direção \(y\).
A expansão ou escalonamento, figura 6, na direção y, função \(g(x)\), pode ser obtida da função \(f(x)\) pela multiplicação da própria função por um fator \(k=\frac{b}{f(a)}\):
\[g(x)=\frac{b}{f(a)}f(x)\]
Exercícios
1. Tomando como base a função \(f(x)=x^2\), definida no intervalo \([0,1]\), encontre a função \(g_A(x)\), definida no intervalo \([0,\frac{\beta}{2}]\), que é o resultado de uma expansão de \(f(x)\) na horizontal, seguida e de uma expansão na vertical, ficando \(g_A(\frac{\beta}{2})=\frac{h}{2}\).
2. A partir da função \(g_A(x)\), obtida no exercício anterior, obtenha a função \(g_B(x)\) que é consequência de um espelhamento em \(y\), mais um espelhamento em\(x\), mais um deslocamento em \(x\) de \(\beta\) e, por fim, um deslocamento em \(y\) de \(h\).
3. Tomando como base a função \(f(x)=1-\sqrt{1-x^2}\), definida no intervalo \([0,1]\), encontre a função \(p_A(x)\), definida no intervalo \([0,\frac{\beta}{2}]\), que é o resultado de uma expansão de \(f(x)\) na horizontal, seguida e de uma expansão na vertical, ficando \(p_A(\frac{\beta}{2})=\frac{h}{2}\).
4. A partir da função \(p_A(x)\), obtida no exercício acima, obtenha a função \(p_B(x)\) que é consequência de um espelhamento em \(y\), mais um espelhamento em\(x\), mais um deslocamento em \(x\) de \(\beta\) e, por fim, um deslocamento em \(y\) de \(h\).
5. Esboce um gráfico, simulando uma função \(f(x)\) qualquer e, em seguida esboce, preferencialmente em outra cor, o gráfico da função \(g(x)=f(\left | x \right |)\) e determine se esta nova função \(g(x)\) assim definida, não poderia ser utilizado como base para o espelhamento de funções na vertical.
6. Da mesma forma que no exercício anterior, analise a possibilidade de se utilizar a função \(g(x)=-\left | f(x) \right |\) como base para o espelhamento de funções na horizontal.