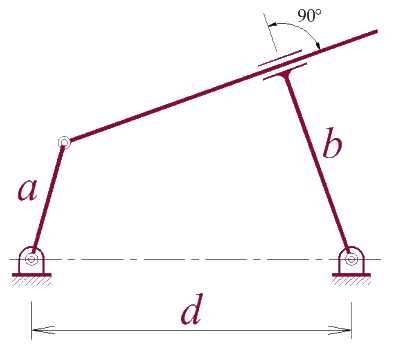
1. No mecanismo, mostrado na figura, são conhecidos o deslocamento angular, a velocidade angular e a aceleração angular da barra \(a\), determine o deslocamento e a velocidade angular da barra \(b\) em função apenas das coordenadas generalizadas da barra \(a\).
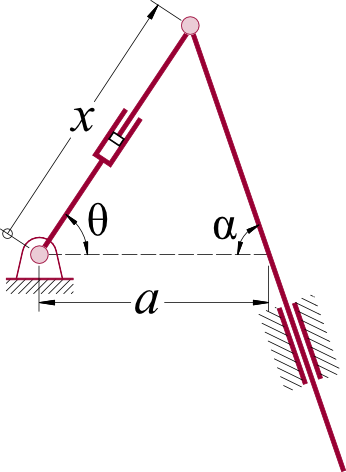
2. Na cadeia abaixo a coordenada principal é \(\theta\), determine o deslocamento, velocidade e aceleração para a coordenada \(x\).
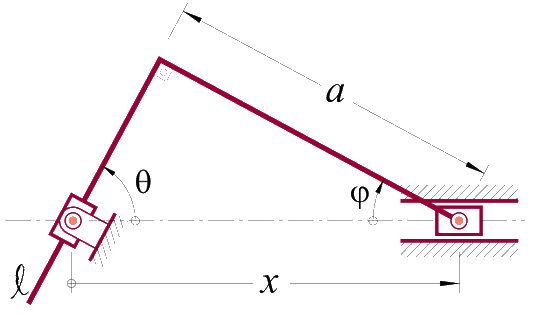
3. No mecanismo mostrado, a barra \(\ell\) forma um ângulo, constante, de 90o na sua parte superior. Verifique se a aceleração do pistão horizontal pode ser dada por:
\[
\ddot x=k_x \left [ \ddot\theta-2\dot\theta^2\frac{1+\cos^2\theta}{\text{sen}\,2\theta} \right ]
\]
4. No mecanismo mostrado, são conhecidos o deslocamento, velocidade e aceleração do pistão horizontal. Determine a aceleração do pistão vertical, sabendo que a barra que une os dois pistões tem comprimento \(a\). Para este problema, as coordenadas generalizadas são apenas (\(x, y\)).
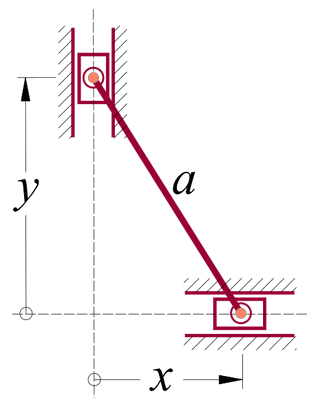
5. Considerando que a entrada se faz pelo pistão vertical, determine a velocidade relativa entre os dois pistões horizontais sem a utilização de coordenadas generalizadas angulares.
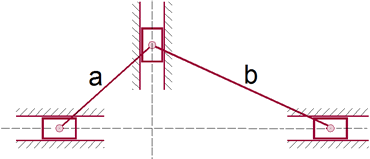
6. Na plaina limadora, sendo \(\theta\) a coordenada principal, determine a velocidade secundária \(\dot x\).
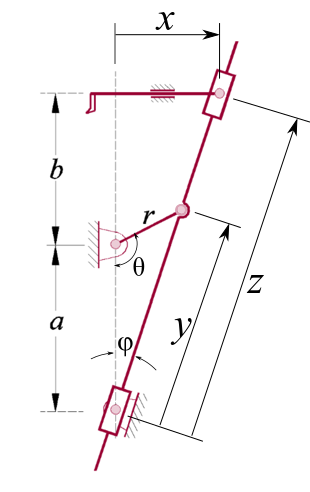
7. No mecanismo abaixo, a coordenada \(x\) é a principal, quando \(\varphi_1=\varphi_2=\varphi\) (matriz 3 x 3), determine o valor de \(k_y\).

8. No mecanismo abaixo, a coordenada principal é \(\theta\). determine o coeficiente de velocidade para a coordenada (\beta). Atente para que, nas expressões desenvolvidas, não surjam novas variáveis que não \(\theta\), \(\alpha\), \(\beta\) e \(x\).
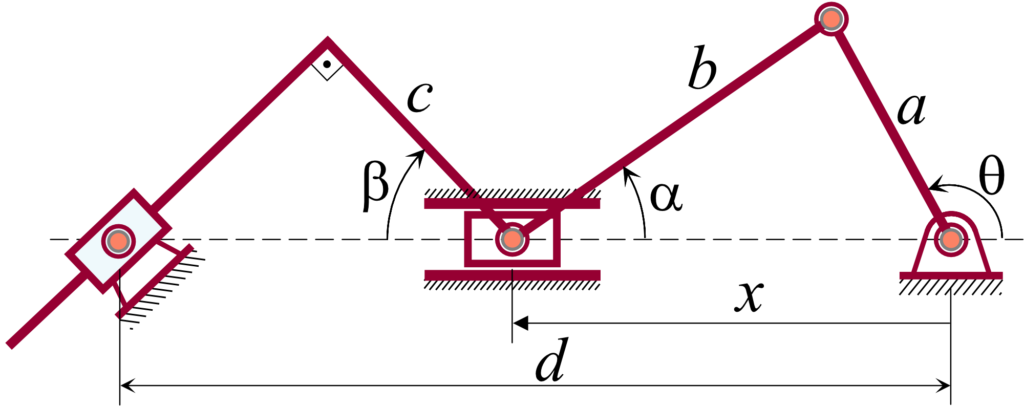
9. No mecanismo abaixo, a coordenada principal é \(\theta\). determine o deslocamento e o coeficiente de velocidade para a coordenada \(y\).
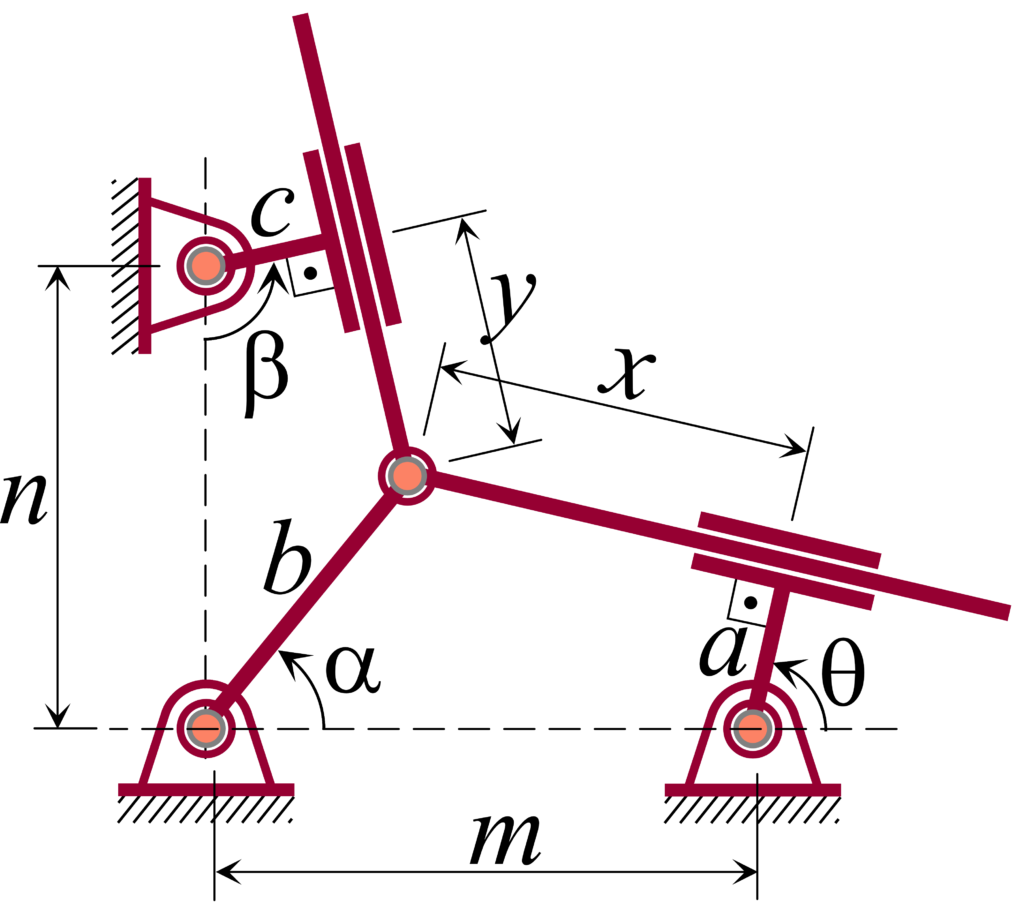
10. No mecanismo abaixo, a coordenada principal é \(y\). determine o deslocamento, a velocidade e a aceleração para a coordenada secundária \(x\). Atente para que nas expressões tenham-se apenas as constantes \(a\) e \(b\) e as coordenadas \(\theta\), \(y\) e \(x\).

11. Considerando o produto \(a\cdot b=24\,cm^2\), para uma velocidade de entrada constante \(\dot{x}=15\frac{cm}{s}\). Determine o valor da acelaração \(\ddot{y}\) (\(\frac{cm}{s^2}\)), quando \(x=3\,cm\).
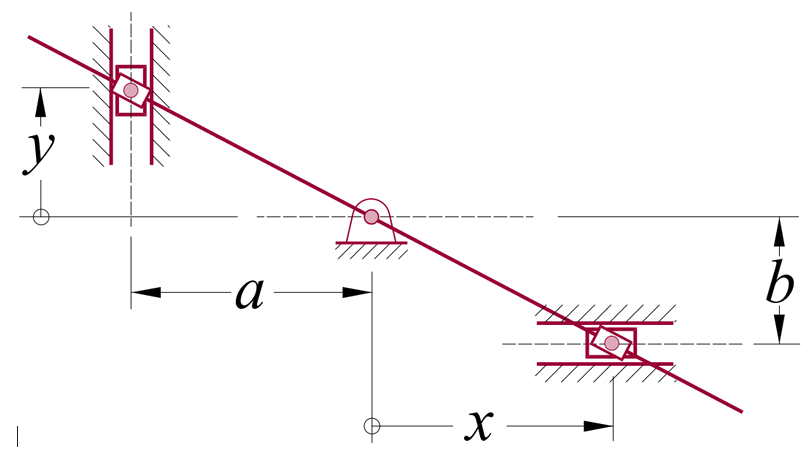
12. No mecanismo, a coordenada \(x\) é principal. Determine os coeficientes de velocidade e aceleração para a coordenada \(y\).
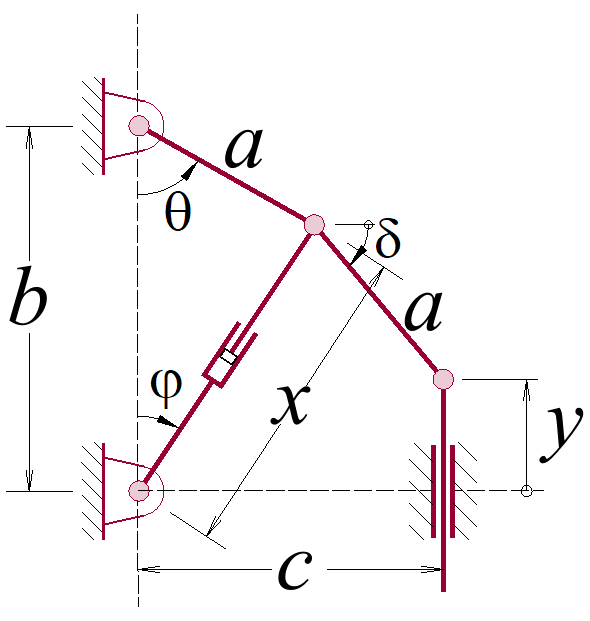
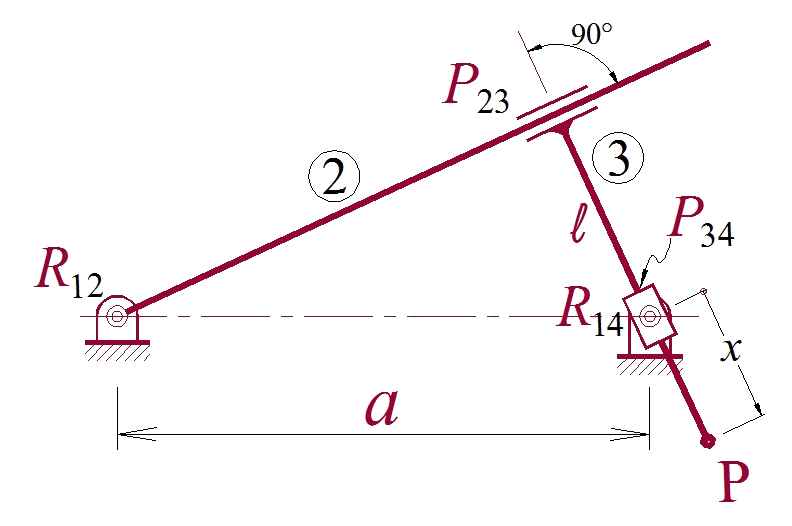
13. No mecanismo, mostrado, a barra 2 recebe a entrada, sabendo-se que a barra 3 tem comprimento \(\ell\), determine, em função da coordenada principal, a velocidade e a aceleração para a variável \(x\) que representa a distância do par cinemático \(R_{14}\) até o Ponto P, utilizando coeficientes de velocidade e aceleração como vistos em sala de aula.