1. Considerando a esteira e a cabine/corpo do trator fixos (represente-os apenas como uma barra fixa simplificada), faça um esboço esquemático do mecanismo, classificando cada barra e aplique Grübler determinando a quantidade de graus de liberdade.

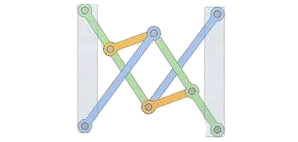
2. Para a cadeia mostrada, a barra horizontal inferior é fixa. Identifique cada barra, classificando-a (binária, tenária, etc.) e, após isto, utilize Grübler para determinar o número de graus de liberdade.
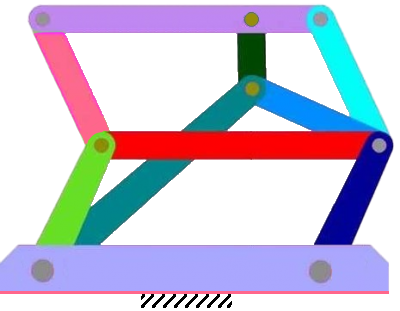
3. Para a cadeia mostrada, considere o carrinho fixo. já sabemos que barras que não apresentam movimento relativo entre si, se constituem na mesma barra, desta forma o mecanismo é totalmente plano, também pares rotativos que têm o mesmo eixo de rotação são o mesmo par. Desta foram, Identifique cada barra, classificando-a (binária, ternária, etc.) e em que permutação ela se enquadra, após isto, utilize Grübler para determinar o número de gruas de liberdade desta cadeia.

4. O sistema físico é composto de duas barras binárias, livres no plano, contendo elementos cinemáticos do tipo rotativo e prismático. Inicialmente determine um sistema de coordenadas generalizadas para as mesmas e, em seguida monte o par prismático (como em b) e determine a quantidade de equações de restrição e informe quantos graus de liberdade este par retira do sistema.
Dica: Para facilitar a resolução, é conveniente se colocar a referência da barras 2 no centro do elemento prismático.
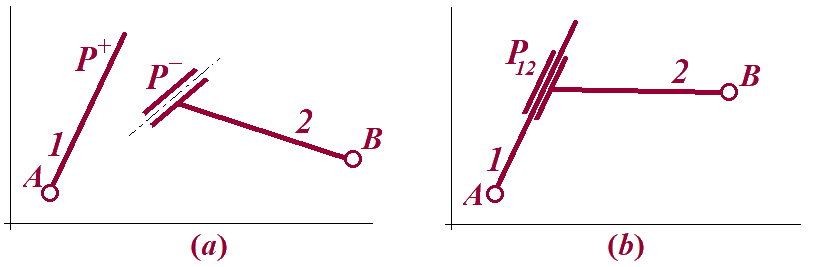
5. Atribua um sistema de coordenadas generalizadas para o sistema em (a), de tal forma que não se tenha equações de restrição nesta atribuição e, após isto monte a restrição mostrada em (b) e determine todas as equações de restrição L.I.
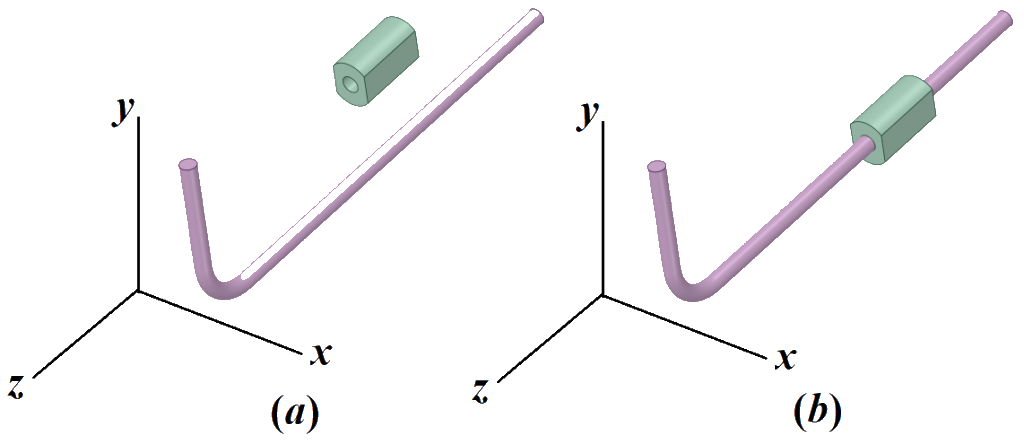
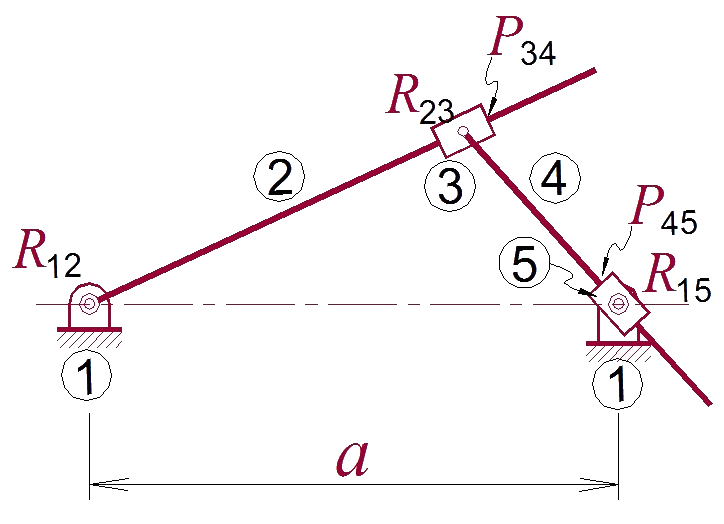
6. Para a cadeia mostrada abaixo, constituída das barras 1, 2, 3, 4 e 5 devidamente conectadas formando os seus respectivos pares cinemáticos, determine um sistema de coordenadas generalizadas conveniente e, a partir deste sistema, considere a criação de uma restrição pela soldagem da barra 3 à barra 4. Para esta nova situação, encontre as equações de restrição e determine o número de graus de liberdade do novo sistema.
7. Na figura, as duas rodas sempre estarão em contato com as suas respectivas paredes, monte um sistema de coordenadas generalizadas conveniente e, em função deste, a partir da quantidade de equações de restrição determine o número de graus de liberdade.
8. Verifique quantas barras tem o mecanismo de “Klann” mostrado abaixo, classifique-as e aplique Grübler para o mesmo. Verifique ainda, se for o caso, em que permutação ele se enquadra e quantas montagens ter-se-ia dentro desta permutação.
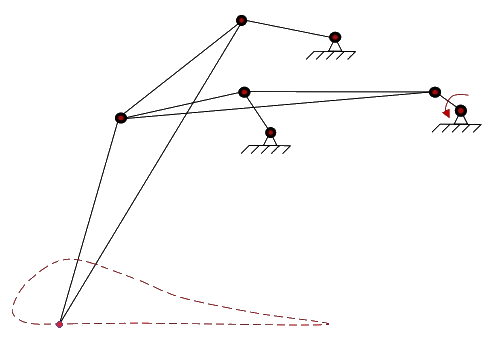
9. Classifique as cadeias cinemáticas abaixo e determine a quantidade de graus de liberdade de cada uma utilizando os conceitos de graus de liberdade vistos no item “Coordenadas Generalizadas”.
OBS. Sob hipótese alguma se deve utilizar Grübler neste problema.
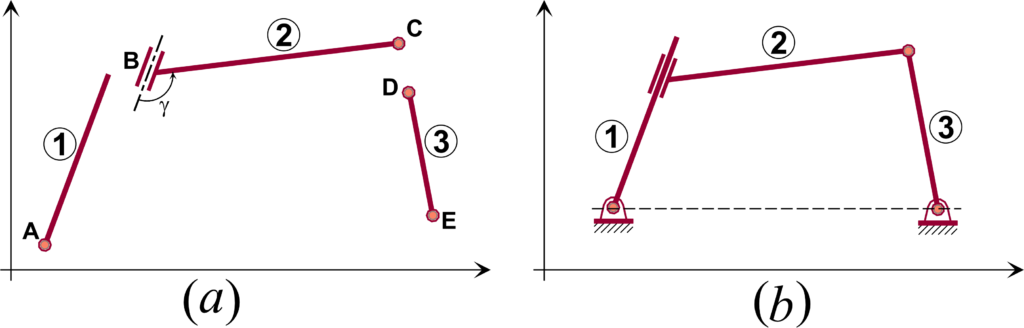
10. Nas figuras abaixo, inicialmente temos, em (a), as barras 1, 2 e 3 livres no plano, monte um sistema de coordenadas generalizadas para esta situação e em seguida efetue as restrições mostradas em (b), determine as equações de restrição decorrentes e diga quantos graus de liberdade o sistema terá após a montagem destas restrições. Considere \(\ell_2\) e \(\ell_3\) os comprimentos das barras 2 e 3 respectivamente e que o ângulo \(\gamma\) é constante na barra 2.
11. Nas figuras abaixo, inicialmente temos, em (a), as barras 1, 2, 3 e 4 livres no plano, monte um sistema de coordenadas generalizadas para esta situação e em seguida efetue as restrições mostradas em (b), determine as equações de restrição decorrentes e diga quantos graus de liberdade o sistema terá após a montagem destas restrições. Considere \(\ell_1\) e \(\ell_2\) os comprimentos das barras 1 e 2, respectivamente.
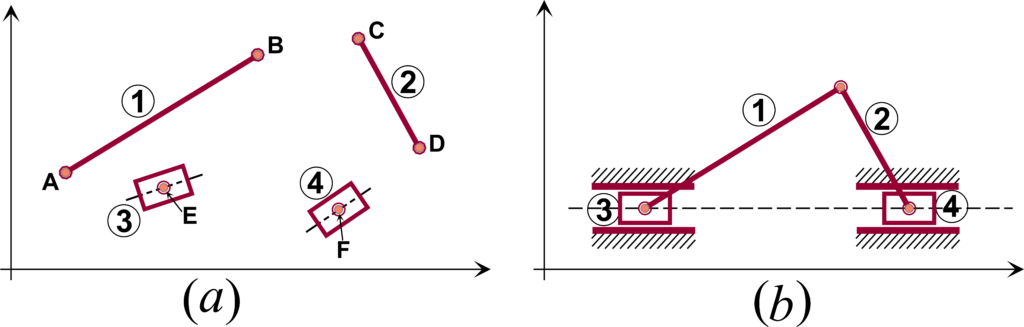
12. Na figura, a roda gira, sem deslizamento, sobre o plano (\Sigma) e impulsiona um cilindro através da barra de comprimento (\ell). Monte um sistema de coordenadas generalizadas conveniente e a partir deste determine a quantidade de graus de liberdade.
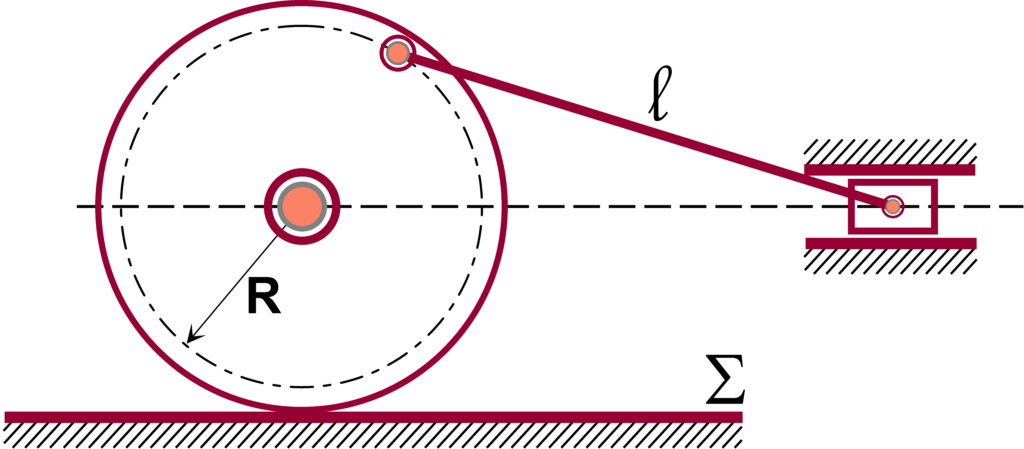
13. Na figura abaixo o ângulo \(\varphi\), entre os eixos dos dois pistões, é constante. Construa um sistema de coordenadas generalizadas contendo uma coordenada para cada barra, excetuando-se a barra fixa, e determine todas as equações de restrição (L.I.) existentes.
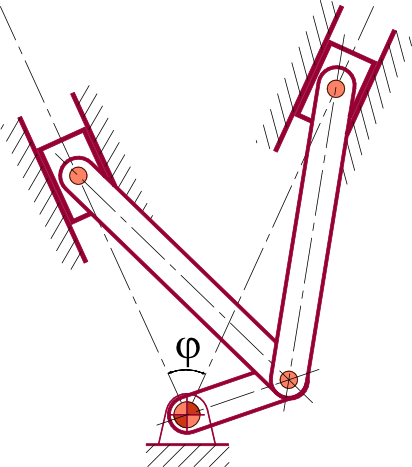
14. Esboce cadeias, impostas,com 3, 4 5 e 6 barras que contenham pelo menos um par superior (plano) do tipo “h“, mostrado abaixo e mostre que este par tem apenas um grau de liberdade.
15. Para a cadeia espacial, mostrada abaixo, determine a quantidade de barras e tente desenvolver um critério de Grübler espacial específico para determinar a sua quantidade de graus de liberdade.
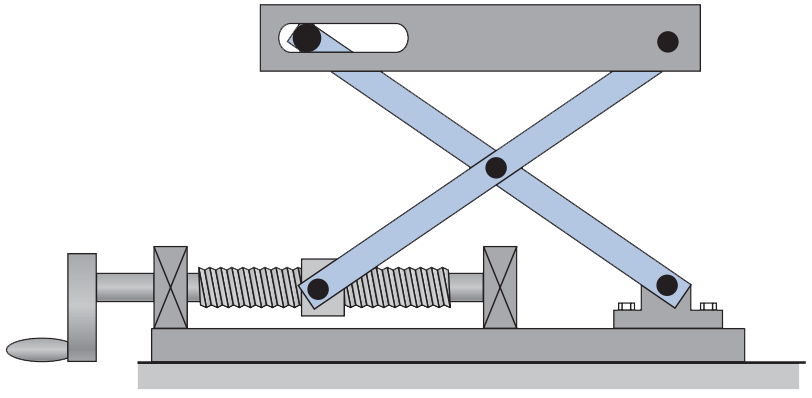
16. Na cadeia abaixo, classifique as barras, com relação à quantidade de elementos cinemáticos e, considerando uma das barras fixas, utiliza Grübler para determinar o número de graus de liberdade.