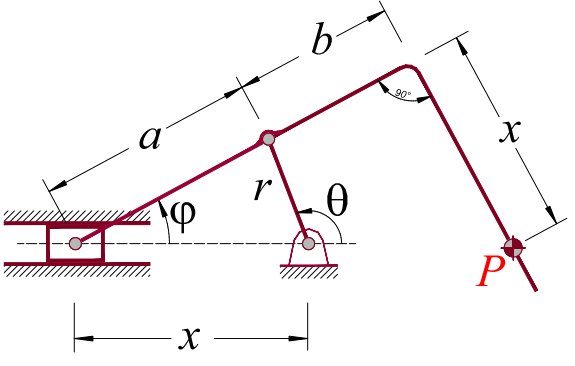
1. No mecanismo da figura, determine o deslocamento, velocidade e aceleração do ponto P, utilizando, para coordenadas generalizadas, somente o sistema (\(\theta,\varphi\)).
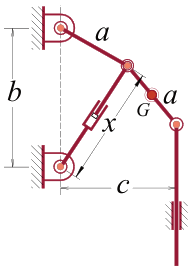
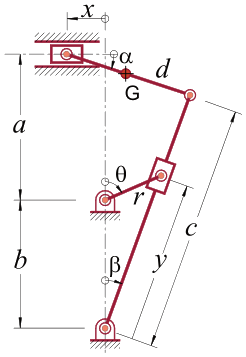
2. Na figura mostrada a seguir, sabendo-se que a entrada se faz pelo pistão, coordenada “x”, arbitre outras coordenadas generalizadas, que se façam necessárias, e determine a velocidade do centro de massa da barra “a”, ponto “G”.
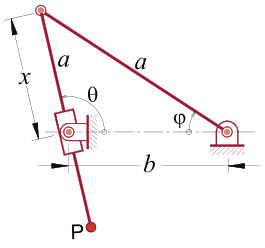
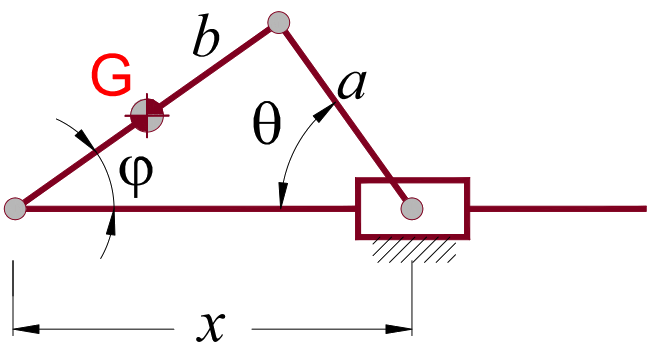
3. Na figura, as coordenadas generalizadas são (\(\theta,\varphi, x\)) e as duas barras têm o mesmo comprimento “a”, determine o deslocamento, velocidade e aceleração para o ponto “P”.
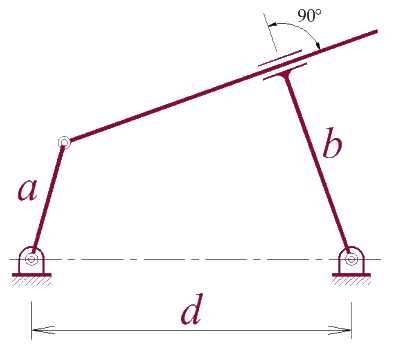
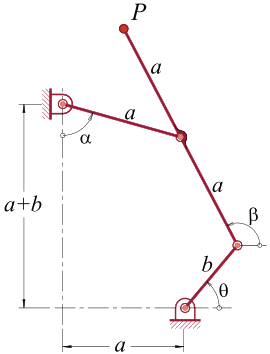
4.No mecanismo dado, as coordenadas generalizadas são (\(\theta, \alpha, \beta\)). Quando a barra “b” se alinhar com a barra acopladora (\(\theta = \pi/2\)) mostre que a velocidade horizontal do ponto “P” é inversamente proporcional à velocidade angular da barra “b”.
5. No problema da figura, o ponto acoplador se situa na extremidade direita da barra “c”. Obtenha a equação da curva descrita por este em coordenadas cartesianas e determine sua velocidade tangencial em cada ponto desta curva.

6. Na plaina limadora mostrada na figura, a velocidade da manivela é constante. Determine a aceleração do centro de massa G, da barra “d” que acopla o balancim ao torpedo.
7. Na figura, sendo \(x\) a coordenada principal, determine a velocidade e a aceleração do centro de massa da barra b. Havendo velocidades e acelerações secundárias nas expressões finais, estas têm que ser estabelecidas.
8. No mecanismo mostrado, o ponto P desliza sobre a barra ficando sempre a uma distância x (variável) da quina (joelho a 90º) desta. Nesta situação determine o deslocamento, velocidade e aceleração deste ponto.
9. No mecanismo a barra (a) recebe o movimento através da coordenada \\(\theta\). Determine o deslocamento, velocidade e aceleração para o ponto “P” do acoplador.
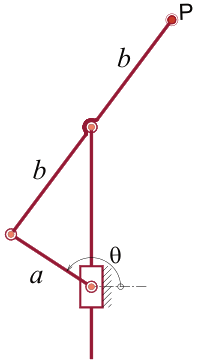
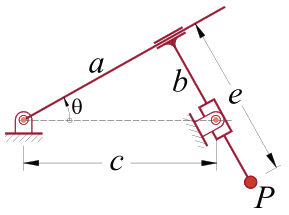
10. No mecanismo a barra “a” se mantém perpendicular à barra “b”, a barra “b” tem comprimento “e” e a barra “a” recebe o movimento de entrada. Verifique se as equações abaixo, que determinam os coeficientes da aceleração para o ponto “P” estão corretas.
\left\{\begin{array}{ll}
\ell_{x_p}=-2c-(e-4c\,\text{sen}\,\theta)\,\text{sen}\,\theta\\
\ell_{y_p}=-(e+4c\,\text{sen}\,\theta)\cos\theta
\end{array}\right.